Math questions / Land and building dimensions
What are the various uses of a school and how are these parts arranged on its site?
Geometry is one of the most important math skills used by architects, engineers, and landscape architects when designing a new building or landscape. Being able to think critically about shapes and forms plays a role in such tasks as calculating the area and perimeter of a structure or determining how many plants will fit on a green roof. This set of math questions investigates the Nueva School buildings and the nearby athletic field (seen below).

1.
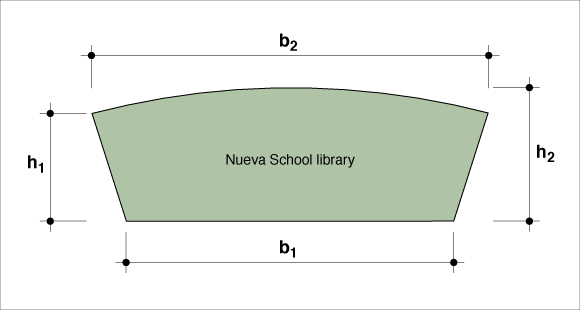
In plan view, the approximate shape of the Nueva School library building is a trapezoid.
The formula for the area of a trapezoid is:
![]()
Calculate the area of the library building in plan view, if:
h1 = 33 feet
h2 = 10 feet
b1 = 135 feet
b2 = 163 feet
2.
When calculating the area of the roof in plan view, would you use the value of h1 or h2 as the correct height? Why?
3.
If neither h1 nor h2 gives an accurate area, suggest a method to find a more accurate area.
4.
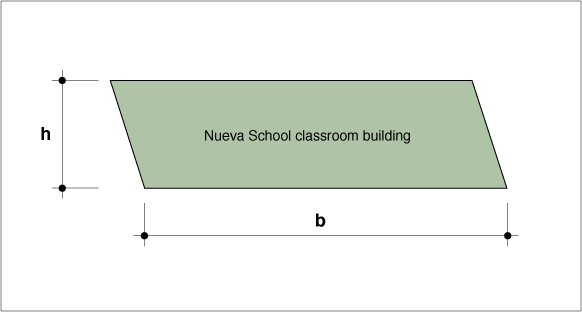
In plan view, the approximate shape of the Nueva School classroom building is a parallelogram.
The formula for the area of a parallelogram is:
![]()
Calculate the area of the classroom building in plan view, if
b = 190 feet
h = 40 feet
5.
Suppose that the Nueva School is hoping to acquire a new rectangular piece of property measuring 60 feet x 40 feet as an addition to the school campus. The diagram below represents a birds-eye view of that plot of land which currently contains 6 trees—shown as tangent circles with their centers spaced 20 feet apart. Find the percentage of the rectangle covered by the circles.

6.
Given the same plot of land, suppose smaller trees were planted so that their centers were spaced 5 feet apart? Find the percentage of the rectangle covered by these trees in this example. Compare your results with your answer in question 5.
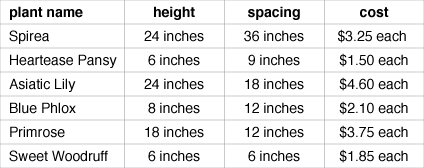
Suppose that you have been hired to work with the landscape architect to redesign the flowers and plants around the main entrance to the Nueva School. Below is a list of possible native California flowers you could use. Each flowerbed measures 10 feet x 2 feet. Keep in mind that the plants you choose for the flowerbed cannot overlap.
Spacing between plants (as shown the chart below) is measured as the distance from the center of one plant to the center of the next plant. This means, for example, that the Spirea plant has a radius of 18 inches.
7.
In plan A, your first idea is to plant only one type of flower. You’ve chosen a total of 6 Asiatic Lilies for each flower bed. How much linear space will be used in each flower bed?
8.
What is the total cost of flowers for plan A?
9.
In plan B, your second idea is to plant two types of flowers. You’ve chosen 6 Sweet Woodruff flowers and 6 Primroses, placing the 6 smaller plants in the middle and 3 of the larger plants on either side. How much linear space have you used?
10.
What is the total cost of flowers for plan B?
11.
Suppose you have a budget of $2,500 to purchase Spirea and Asiatic Lilies, and you must have twice as many Asiatic Lilies as Spirea. What is the maximum number of each flower you will be able to buy?
12.
Find the total cost of a flower purchase, if you need twice as many Blue Phlox as Spirea. The total of Spirea and Heartease Pansy is 62, and the number of Heartease Pansy is two more than twice the Blue Phlox.
13.
Given flower bed dimensions of 18 feet by 4 feet and a budget of $115, create your own plan to plant this flower bed using the selection of plants given above. No overlap is allowed in planting the flowers, you must cover as much area as possible, and you must use as much of the budget money as possible.
Use the diagram below to answer the following questions. Suppose that the Nueva School decides to put a 20-foot wide gravel jogging path around the perimeter of their sports field which measures 320 feet x 120 feet. The path will need to be excavated and leveled, and framing will be installed to hold the gravel in place.
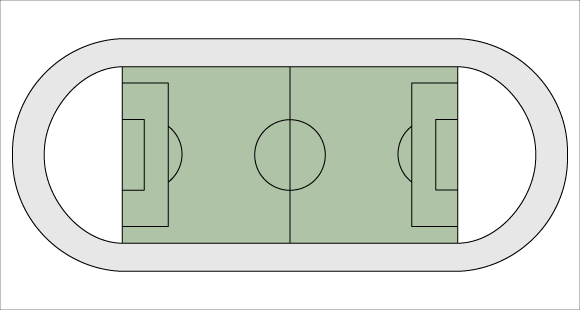
14.
How many linear feet of framing will be needed? (Hint: Calculate both the inside and outside perimeters of the gravel jogging path.)
15.
What is the total area of the gravel path?
16.
If the path is filled with gravel that is 3†deep, how many cubic yards of gravel will be needed?
17.
Suppose the cost for labor and materials for this job is $12.50 per square yard. What will the overall cost be for the path?